Neural Decomposition: Functional ANOVA with Variational Autoencoders
Abstract
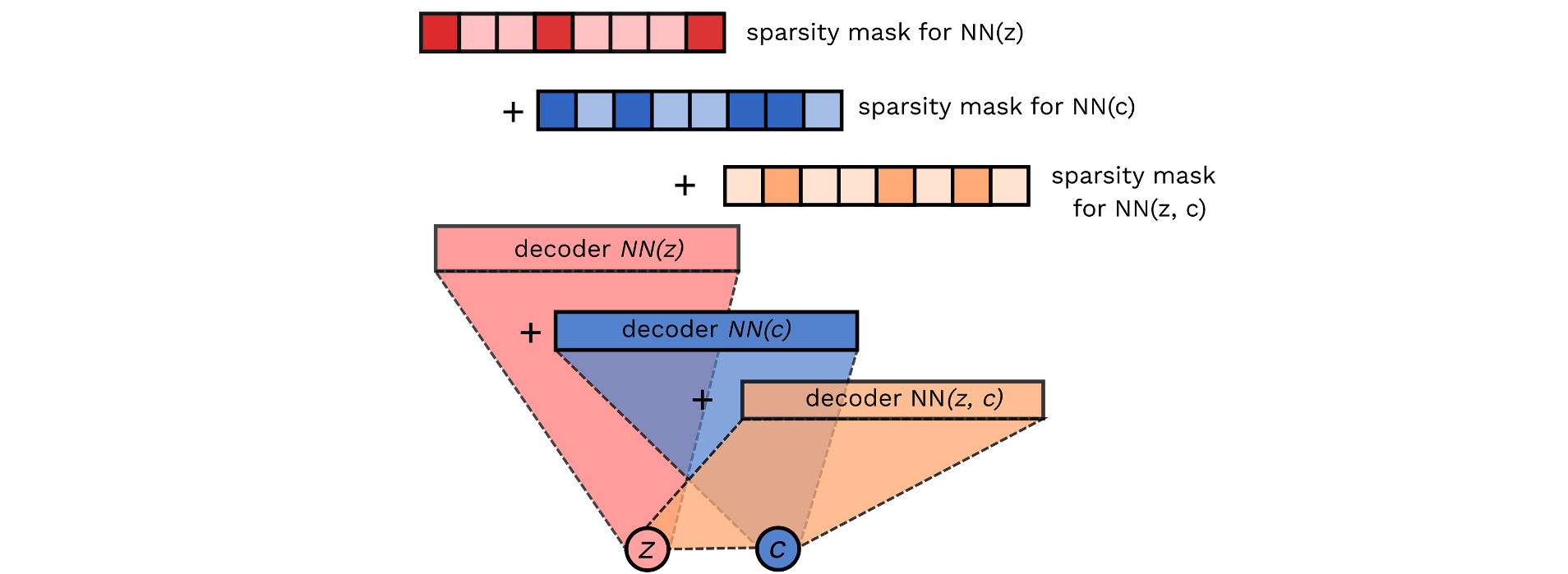
Variational Autoencoders (VAEs) have become a popular approach for dimensionality reduction. However, despite their ability to identify latent low-dimensional structures embedded within high-dimensional data, these latent representations are typically hard to interpret on their own. Due to the black-box nature of VAEs, their utility for healthcare and genomics applications has been limited. In this paper, we focus on characterising the sources of variation in Conditional VAEs. Our goal is to provide a feature-level variance decomposition, i.e. to decompose variation in the data by separating out the marginal additive effects of latent variables z and fixed inputs c from their non-linear interactions. We propose to achieve this through what we call Neural Decomposition - an adaptation of the well-known concept of functional ANOVA variance decomposition from classical statistics to deep learning models. We show how identifiability can be achieved by training models subject to constraints on the marginal properties of the decoder networks. We demonstrate the utility of our Neural Decomposition on a series of synthetic examples as well as high-dimensional genomics data.