Decomposing feature-level variation with Covariate Gaussian Process Latent Variable Models
Abstract
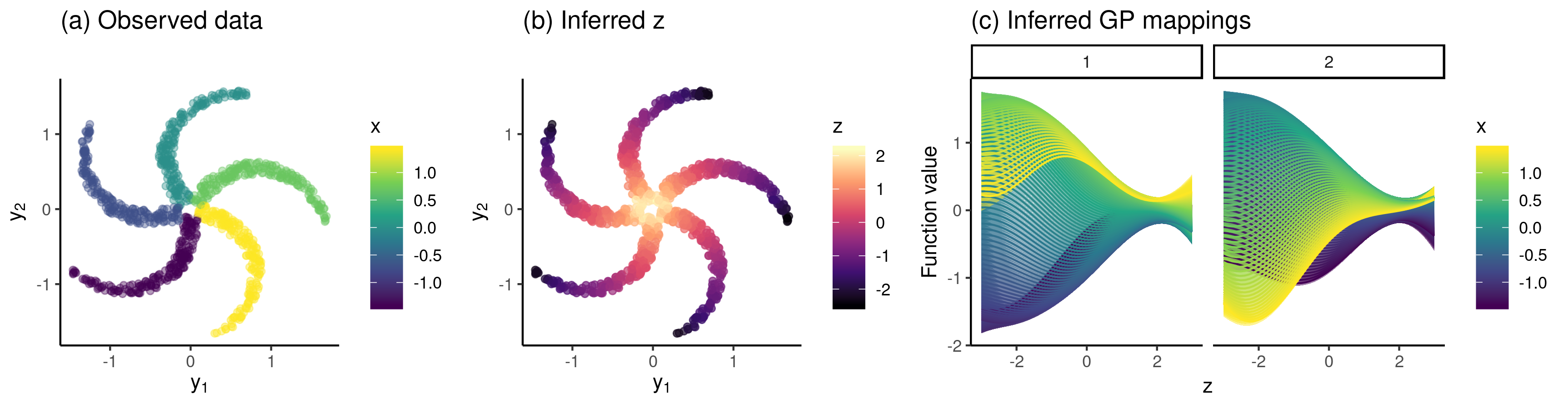
The interpretation of complex high-dimensional data typically requires the use of dimensionality reduction techniques to extract explanatory low-dimensional representations. However, in many real-world problems these representations may not be sufficient to aid interpretation on their own, and it would be desirable to interpret the model in terms of the original features themselves. Our goal is to characterise how feature-level variation depends on latent low-dimensional representations, external covariates, and non-linear interactions between the two. In this paper, we propose to achieve this through a structured kernel decomposition in a hybrid Gaussian Process model which we call the Covariate Gaussian Process Latent Variable Model (c-GPLVM). We demonstrate the utility of our model on simulated examples and applications in disease progression modelling from high-dimensional gene expression data in the presence of additional phenotypes. In each setting we show how the c-GPLVM can extract low-dimensional structures from high-dimensional data sets whilst allowing a breakdown of feature-level variability that is not present in other commonly used dimensionality reduction approaches.